Results summary

Now that the thermal behaviour of the sample is known, having a thermal conductivity of 2 \ W/m \cdot K, in both configurations of the support and in each of the operating temperatures that have been studied, now the variation of the temperature gradient obtained with the modified support will be plotted. It will be shown, in red, the absolute variations achieved at each of the operating points and, also, the relative variations (in percentage), in blue. It will be done, not only for the case of \lambda_{sample} = 2 \ W/m \cdot K , but for all the conductivities considered in this thesis, this is, for \lambda_{sample}= 2 \ W/m \cdot K,\lambda_{sample}= 20 \ W/m \cdot K  and  \lambda_{sample}= 100 \ W/m \cdot K.

Besides the plots of the variation of the temperature gradient in the sample it will be also plotted the mean temperature variation obtained in the sample, proving, this way, that the ensemble has a higher energy efficiency when the new support is used.

 

Sample conductivity of 2 W/m·K

k2_gradient
Plot of the variation of the temperature gradient obtained with the new support for the whole operating range of the heating device

This plot summarizes the results mentioned in the last section. It can be seen, in red, that the greatest gradient reductions in the sample are obtained at low operating temperatures, reaching values that exceed 16ºC. As the operating temperature rises, the gradient reduction obtained in the sample is lower; however, the relative variation, that indicates the effectivity of the new support, keeps increasing. This fact can be explained by the thermal conductivity of alumina. The thermal conductivity of this material has a strong dependency with temperature, specifically, as the temperature rises the thermal conductivity of alumina decreases considerably. This drop in the thermal conductivity makes the alumina tube have a more insulating behaviour at high temperatures than at lower temperatures, being more important, in absolute value, the effect of the change in the tube geometry at lower temperatures, since at high temperatures the drop of the thermal conductivity of alumina itself reduces considerably the temperature gradient in the sample.

k2_T
Plot of the mean temperature variation of the sample obtained with the new support for the whole operating range of the heating device

It can be noticed that the use of the new support has a positive impact on the ensemble energy efficiency for the whole operating range of the heating device, obtaining the greatest benefits at low operating temperatures. The reason of this decrease on the benefit as temperature rises is the same that has been mentioned in the previous plot: the noticeable drop in the thermal conductivity of alumina at high temperatures causes that the benefits of the new support have a minor importance at high operating temperatures.

 

Sample conductivity of 20 W/m·K

qw
Plot of the variation of the temperature gradient obtained with the new support for the whole operating range of the heating device

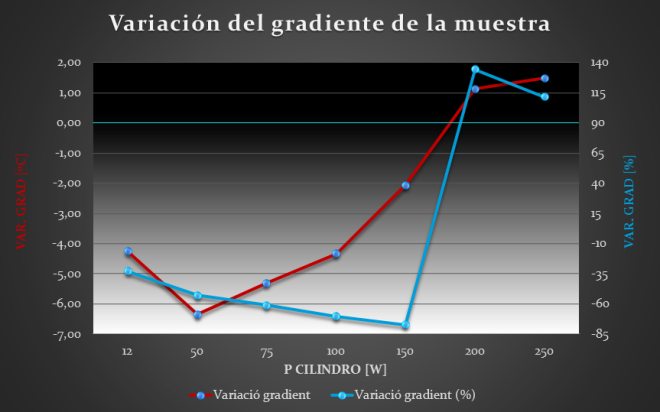
For the case of a sample with thermal conductivity of 20 W/m·K it is obtained the plot shown on the left (or above). It is noticed that the curves have a very similar shape to the previous ones; however, the main difference between both plots is found in the absoulte value of the gradient variation achieved in each case. As it can be noticed in the left column, the maximum values of variation are also achieved at low operating temperatures; however, due to the higher thermal conductivity of the sample, the maximum reduction obtained is lower than 7ºC, in front of the 16ºC reduction achieved before. Despite that, the variation in percentage has a very similar curve to the one obtained before, both qualitatively and cuantitatively, which indicates that the solution is equally effective.

Gráfico de la variación de la temperatura media de la muestra obtenida con el nuevo soporte para todo el rango de funcionamiento del dispositivo calefactor
Plot of the mean temperature variation of the sample obtained with the new support for the whole operating range of the heating device

The sample mean temperature variation curve for the case of \lambda_{sample}=20 \ W/ m \cdot K is practically equal to the one obtained for the case of \lambda_{sample}=2 \ W/ m \cdot K. The main difference is that, especially at low operating temperatures, the increment of the sample mean temperature is noticeably higher in this case.

 

Sample conductivity of 100 W/m·K

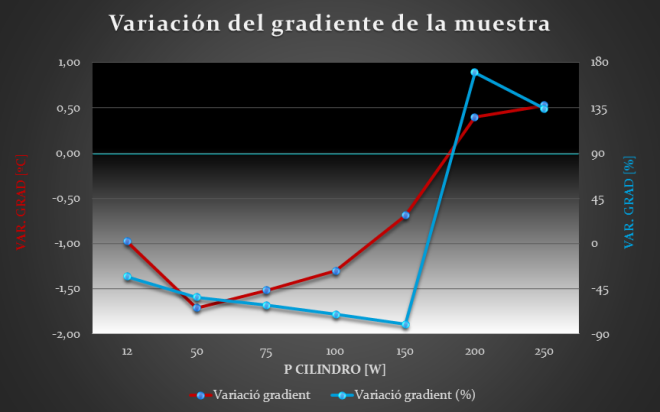
k100_gradient
Plot of the variation of the temperature gradient obtained with the new support for the whole operating range of the heating device

Again, it is noticed that the curves have similar tendencies to the ones obtained in the previous plots. The greatest difference is the magnitude of the thermal gradient variations in the sample, obtaining this time a maximum below 2ºC. This fact, as it has been already said, is due to the sample conductivity, because increasing its value it causes lower thermal gradients in the sample. Thus, using the new support the gradient variation achieved is less significant for high values of sample conductivity. However, if the percentage variation curve is analyzed it can be noticed that it is practically the same that has been obtained in the previous cases, that is to say, the effectivity of the new support is proved.

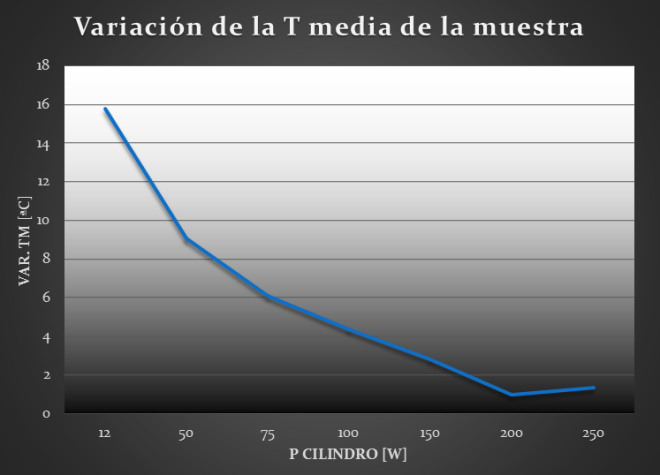
k100_T
Plot of the mean temperature variation of the sample obtained with the new support for the whole operating range of the heating device

The sample mean temperature variation keeps the same tendency. The difference is that the values are slightly higher than the ones obtained in the previous case.

The benefits of the new support are more evident at low operating temperatures. This is due to the variation of the thermal conductivity of alumina, which decreases as temperature rises, that is to say, at high temperatures the low conductivity of alumina exercises the gradient reductive effect desired. Even so the gradient also gets reduced with the new support at high temperatures (until the phenomenon of thermal inversion is reached).

Conclusions